[latexpage]
The crypto market is still inefficient. Cryptoassets have different rates on different exchanges. The big question is how we can profit from that inefficiency. One approach is making transactions between exchanges, but if we buy a cryptoasset on one exchange, by the time we can sell it on another, the price difference may no longer exist. For a discussion of this problem, see What I Have Learned from My Arbitrage Experiences with Cryptoassets.
A more efficient approach is using what I call virtual transactions: buying a pair on one exchange and simultaneously selling this pair in another exchange. In order to use virtual transactions to exploit arbitrage opportunities, you must have funded wallets before profitable oscillations events. In a profitable oscillation event, the price difference for a given pair between two exchanges allows you to make profit using two virtual transactions. The first virtual transaction at the time of the event and the opposite operation once the event dissapears and the price difference returns to average values in a considered period.
Put in mathematical terms:
\begin{equation*}
N \left\{ \left[ bid_1^I (1-fee_1) – ask_2^I (1+fee_2) \right] + \left< \left[ bid_2^{II} (1-fee_2) – ask_1^{II} (1+fee_1) \right] \right> \right \} \quad > \quad 0
\end{equation*}
where $N$ is the amount of assets you are exchanging, $ask$ refers to the values you would pay buying these assets, $bid$ refers to the values you would receive selling these assets, the sub-indices $1$ and $2$ refers to the two exchanges and the supra-indices $I$ and $II$ refers to the first and second virtual transactions. The $\left< \cdot \right>$ operator is used to average the values in a given period. This method is a statistical arbitrage method known as pair trading and works using co-integrated pairs. For a deeper look into pair trading algorithms, see Introduction to Pairs Trading. Most arbitrage only monitor for price differences and is just a particular case of this method, considering the second half of the equation equal to zero.
Statistical arbitrage has its risks, since it is necessary to hold cryptoassets, unless the chosen exchanges accept a stable currency as collateral for margin trading. Although there is a profit due to arbitrage, there may also be a devaluation of our capital due to market volatility. On the other hand, it is also necessary to hold a quote currency buffer in each exchange to cover price fluctuations.
Some useful tips! Your trading bot should:
- Exploit profitable oscillations events as quickly as possible. Use market type orders and not limit type orders.
- Use leverage whenever possible. Some exchanges like Bitfinex, Huobi, Okex, Kraken and Bitmex allow you to execute your long/short positions with 2x, 3x and even 100x, which allows you to get a higher ROI on the invested capital. Even better, using margin trading, on some exchanges you can keep your collateral in stable coins using a market-neutral strategy.
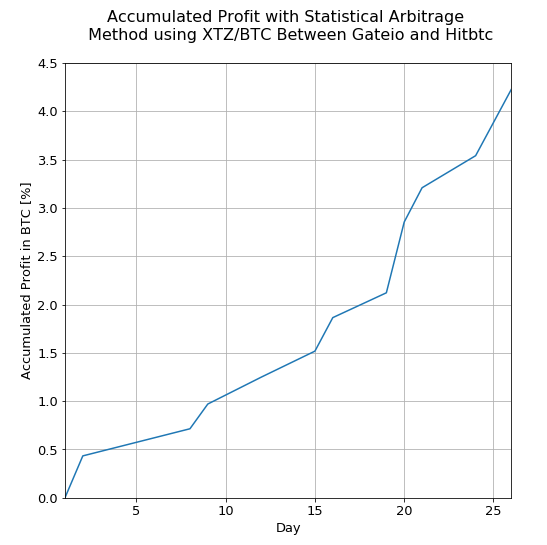
I apply this statistical arbitrage method using the pair XTZ/BTC between the exchanges Gateio and Hitbtc, from 28th August to 23th September 2018. Yo can download the log using this link. I deposited 0.2 BTC on each exchange, and I bought some XTZ on Hitbtc (using exactly 0.15384 BTC). I left some free bitcoins as a buffer (~30%) to cover price volatility in future trades. Each step of the log starts with Opening trades and ends with Closing trades. Opening trades are an XTZ purchase on Gateio and an XTZ sale on Hitbtc, and Closing trades an XTZ sale on Gateio and an XTZ purchase on Hitbtc. The same amount of bitcoins is invested at the beginning of each step. The amount $N$ of XTZ traded on each exchange in a step remains fixed, but can vary between steps. All orders are executed using market type. The ROI of the operations in the period considered is 4.2% of the total BTC initially invested, without considering XTZ valuation changes.
If you liked this article, you might also like:
- What I Have Learned from My Arbitrage Experiences with Cryptoassets.
- Cryptocurrency Backed Lending Platforms
- A Review Of Cryptoasset Valuation Frameworks
- Analizing Blockchain Networks with Metcalfe’s and Odlyzko’s laws
Disclaimer: CoinFabrik does not provide financial advice. This material has been prepared for educational purposes only, and is not intended to provide, and should not be relied on for, financial advice. Consult your own financial advisors before engaging in any investment.