Introduction
One can think of modern cryptography like an engine; different mathematical and computational tools work together to keep cryptography safe for our daily communications.
Just like a car’s timing belt needs to be changed every tens of thousands of miles, cryptography also requires periodic adjustments every few decades to keep its underlying tools functioning correctly.
In particular, the equivalent of a car’s timing belt in the world of cryptography are the keys (public and private) that we use for securing our communications. The act of “running out” seen in the timing belt is analogous to the increasing key length needed to maintain the encryption standards.
In this article, we’ll review one of the key algorithms that form the backbone of modern cryptography—Diffie-Hellman—and show how changing the underlying mathematics turned out to be an elegant solution to keep the cryptographic engine running when the timing belt started to wear out.
Timing Belts and Galois Fields
The cycling of a timing belt in a car ensures that the engine’s valves open and close at the correct times. Similarly, the cyclic properties of Galois Fields, or finite fields, are a fundamental aspect for modern encryption.
Finite fields are like clocks. If we add hours inside a clock and exceed 12 o’clock, we truncate the excess hours to fall again within the clock. This is what is called modular arithmetic.
In modular arithmetic, a base is chosen, say 12, and all arithmetic operations (addition, multiplication, etc.) are truncated against this base using what is called the modulo operation.
For example:
5 modulo 12 = 5
13 modulo 12 = 1
7+8 modulo 12 = 13 modulo 12 = 1
5*7 modulo 12 = 35 modulo 12 = 11
When working on multiplication of two numbers, the modulo operation allows you to define multiplicative inverses that are a bit different from what we are used to in rational numbers.
For example, if we consider the number 2 modulo 5, it turns out that if we multiply it by 3 we obtain 1 modulo 5.
2 * 3 modulo 5 = 6 modulo 5 = 1
That is, 3 is the inverse of 2 modulo 5.
Something else that we can do with numbers within finite fields is to elevate them to powers. Since we are working inside a finite field, there is only a finite number of possible results, the elements of the field (“the hours of the clock”). If when elevating an element of the group to powers, we obtain all the elements of the field (“all the hours in the clock”), we say that that element is a multiplicative generator for the field.
For example, consider the finite field of positive integers modulo 5. The number 2 is a generator of this group, because by elevating it to different powers we obtain all the other members of the group (1, 2, 3 and 4).
2^1 modulo 5 = 2 modulo 5
2^2 modulo 4 = 4 modulo 5
2^3 modulo 5 = 8 modulo 5 = 3 modulo 5
2^4 modulo 5 = 16 modulo 5 = 1 modulo 5
This property of generators leads us to an important concept in cryptography: the Discrete Logarithm Problem (DLP). DLP is like having a clock where the hour hand moves in intervals of many hours instead of one, and trying to find how many times the clock has clicked given that you know its starting and ending position.
Mathematically, given a prime number p, a generator g, and an element h in the field, the DLP asks: find the exponent x such that g^x ≡ h (mod p).
Using our previous example, if someone tells you that 2^x ≡ 3 (mod 5), and asks you to find x, you’d have to try different values until you found that x = 3. This is easy with small numbers, but becomes incredibly difficult with large numbers.
The crucial aspect of the DLP is that it’s easy to compute in one direction (finding h given g, an exponent x, and p) but computationally difficult in the reverse direction (finding the exponent x given g, h, and p) when using large numbers. This asymmetry forms the basis of many cryptographic algorithms, in particular the Diffie-Hellman key exchange.
Diffie-Hellman: An engine with moving parts
Now that we understand the basics of finite fields and the Discrete Logarithm Problem, let’s see how these concepts come together in a real-world cryptographic application: the Diffie-Hellman key exchange.
Imagine Alice and Bob want to agree on a secret key to encrypt their messages, but they can only communicate over an insecure channel where Eve might be eavesdropping. The Diffie-Hellman protocol allows them to do this securely, leveraging the properties of finite fields and the difficulty of the Discrete Logarithm Problem.
Here’s how it works. Alice and Bob publicly agree on a large prime p and a generator g of the multiplicative group modulo p. These are like choosing the size of the clock and how the hour hand moves.
Alice chooses a secret number a, and Bob chooses a secret number b. These are their private keys.
Alice computes A = g^a mod p and sends it to Bob. This is like Alice moving the hour hand of her clock a secret number of clicks and telling Bob where it landed. Similarly, Bob computes B = g^b mod p and sends it to Alice.
Finally, Alice then computes (B^a) mod p, and Bob computes (A^b) mod p. The magic of Diffie-Hellman is that these two computations result in the same value: (g^ab) mod p. This becomes their shared secret key.
The security of this protocol relies entirely on the Discrete Logarithm Problem. Even though Eve can see A and B, she can’t feasibly determine a or b due to the difficulty of solving the DLP for large numbers.
Let’s use a small example for illustration (remember, real-world applications use much larger numbers):
Alice and Bob agree on p = 23 and g = 5.
Alice chooses a = 6, Bob chooses b = 15, these are their private keys.
Alice sends A = 5^6 mod 23 = 8 to Bob.
Bob sends B = 5^15 mod 23 = 19 to Alice.
Alice computes 19^6 mod 23 = 2.
Bob computes 8^15 mod 23 = 2.
They’ve now agreed on the shared secret key 2, without ever directly exchanging this value. This shared secret key can be used by Alice to encrypt a message into a ciphertext and send to Bob, who can then decrypt it using the same shared key. For example, our shared secret 2 could be the number of shifts in the Caesar Cipher. Larger common keys are used in other modern symmetric algorithms like AES.
This elegant use of modular arithmetic and the properties of finite fields allows secure key exchange over insecure channels, forming a crucial part of the engine of modern cryptography. However, even this robust system began to show signs of wear as computational power increased.
A timing belt about to break
Just as a car’s timing belt starts to wear out after thousands of miles, the security of the Diffie-Hellman key exchange began to show signs of strain as computational power increased exponentially over the years.
The security of Diffie-Hellman relies on the difficulty of solving the Discrete Logarithm Problem (DLP) for large numbers. However, as computers became more powerful and new algorithms were developed, the size of the “large numbers” needed to maintain security kept growing.
In our car analogy, this is like stretching the timing belt to keep the engine running smoothly. But just as there’s a practical limit to how long a timing belt can be stretched before it cracks, there’s a limit to how large we can make our prime numbers to keep our communications safe before the computations become too slow for practical use.
To maintain the same level of security, cryptographers have to use increasingly larger prime numbers. For example, in the 1990s, a 512-bit prime was considered secure for Diffie-Hellman. Today in 2024, recommendations have grown to 2048 bits or larger.
This growth in key size led to increased computational cost and slower performance, especially on resource-constrained devices like smartphones or IoT devices. It was clear that, like a stretched timing belt, the integer-based Diffie-Hellman was approaching its limits.
Looking for Spare Parts: Elliptic Curves
Cryptographers needed a new approach – a different mathematical structure that could provide the same security with smaller key sizes. They found this in elliptic curves. Just as a car might switch from a timing belt to a timing chain for better longevity, cryptography was about to make its own upgrade.
What is an elliptic curve? At its core, an elliptic curve is defined by an equation of the form:
y² = x³ + ax + b
- When plotted, this equation creates a smooth, symmetric curve with some interesting properties:
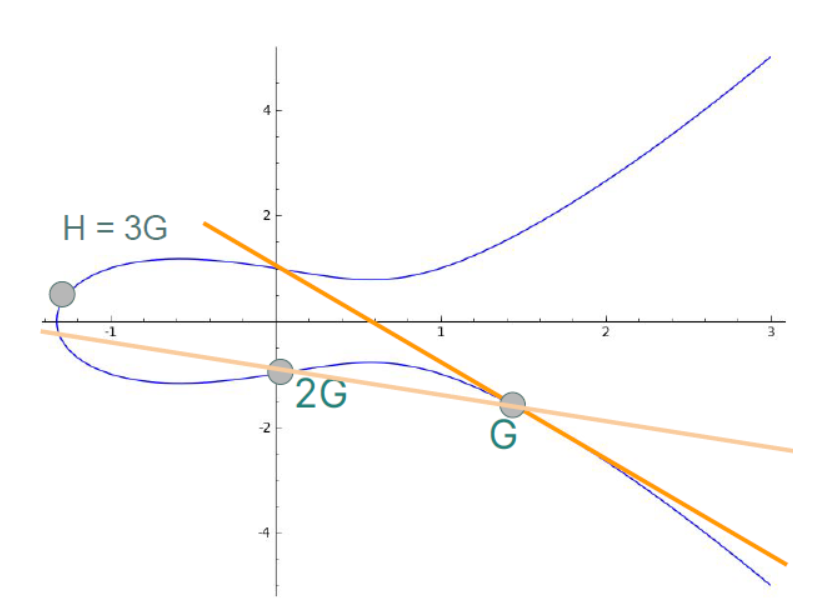
The curve is symmetric about the x-axis, like a mirror image. - Any non-vertical line will intersect the curve at no more than three points.
[Reference Image 2: This Elliptic Curve and its image is taken from the article A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography by Nick Sullivan. Following representations are an adaptation from this image.]
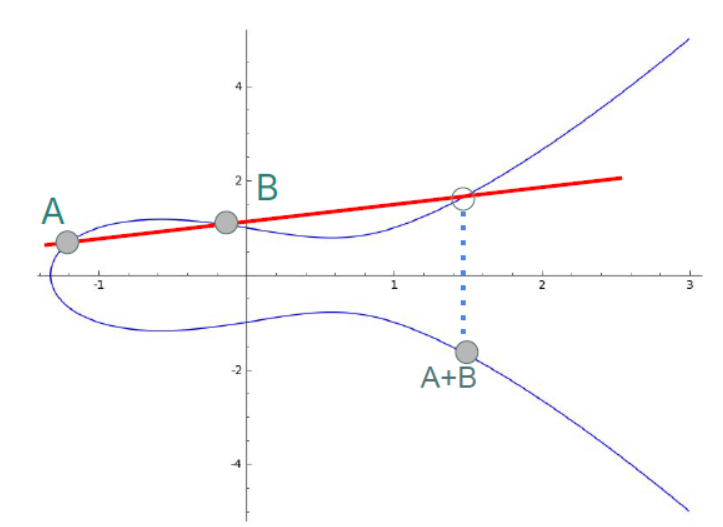
These properties might seem abstract, but they allow us to define a group operation on the curve, much like we did with our clock analogy for finite fields. By defining the addition of points on the elliptic curve, we will be able to formulate an analogous problem to DLP, but for points on the curve.
Here’s how point addition works on an elliptic curve:
- To add two points A and B, draw a line through them.
- This line will intersect the curve at a third point.
- Reflect this point across the x-axis, and you’ve found A + B.
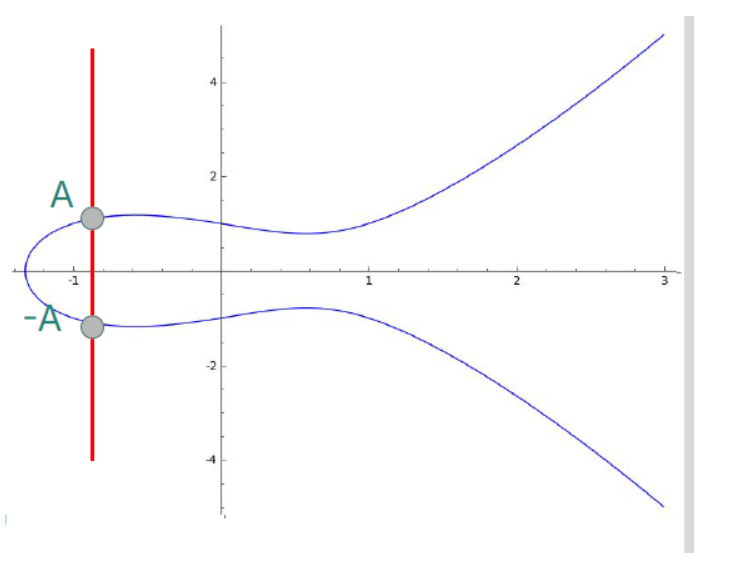
This operation forms the basis of elliptic curve cryptography. It’s commutative (A + B = B + A), associative and has an identity element (a point at infinity that acts like zero). The inverses of points in the curve are simply their symmetrical points across the x axis.
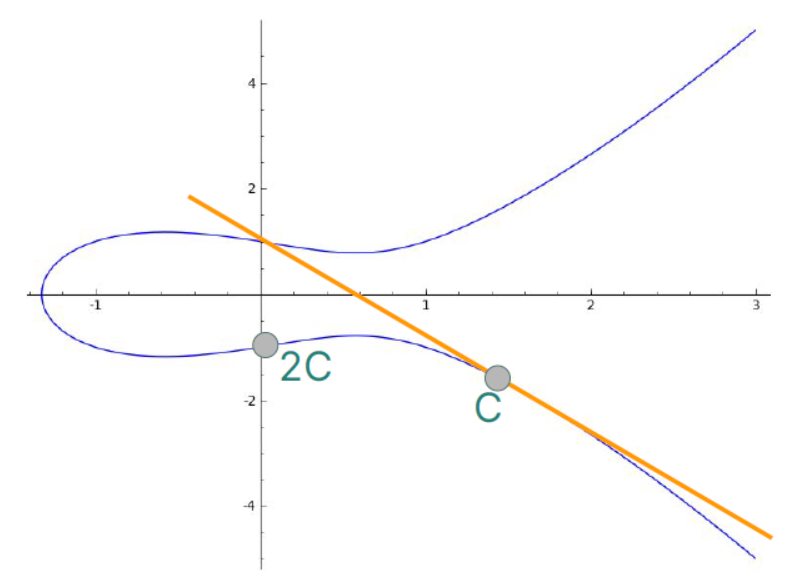
We can also define scalar multiplication: multiplying a point C by an integer n means adding C to itself n times. For this operation, we consider the tangent line at the point C, and continue on step 2 from the adding method described above.
This operation, written as nC, will be the elliptic curve equivalent of exponentiation in our previous formulation of DLP.
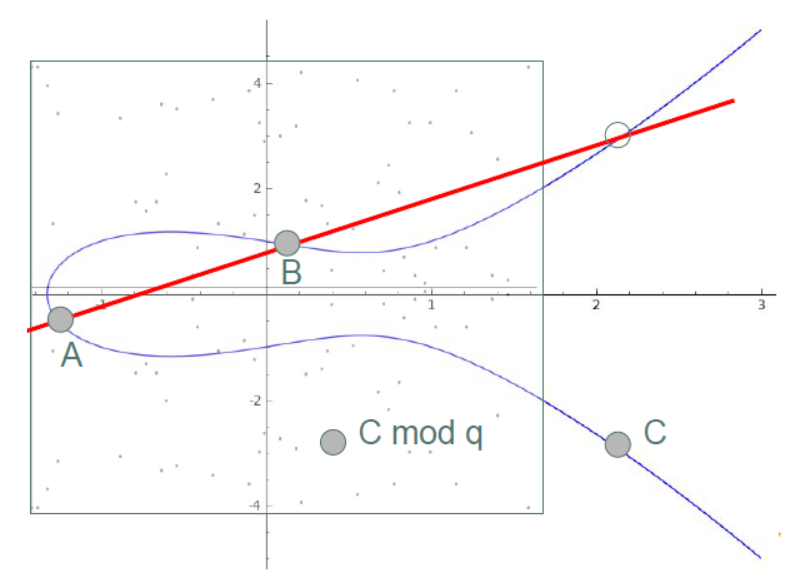
Now, here’s where it gets interesting for cryptography. When we work with elliptic curves over finite fields (where the x and y coordinates are elements of a finite field), the smooth curve becomes a scattered set of points inside a square, as points on the curve wrap around due to the modulo operation forced by the underlying finite field. However, our addition and multiplication operations still work! Take a look at the next graph showing point addition on an elliptic curve over some field F_q (i.e: integers modulo q, where q=p^n with p prime).
With this new group in mind, one can reformulate the Discrete Logarithm Problem for points on the elliptic curve.
The Elliptic Curve Discrete Logarithm Problem (ECDLP) tries to solve the following equation.
Given points G and H on an elliptic curve, find the integer x such that xG = H.
This problem turns out to be even harder to solve than the traditional Discrete Logarithm Problem, allowing us to use much smaller key sizes for the same level of security. For example, a 256-bit elliptic curve key provides security comparable to a 3072-bit RSA key!
Time for an Upgrade (ECDH)
Now, if we replace our worn-out timing belt with a more efficient elliptic curve “timing chain,” we can see how this upgrades our Diffie-Hellman key exchange. The Elliptic Curve Diffie-Hellman (ECDH) follows the same principle as its predecessor but operates in the world of elliptic curves.
Here’s how ECDH works:
- Alice and Bob agree on a specific elliptic curve E and a base point G on that curve. This is analogous to choosing the prime p and generator g in the original Diffie-Hellman.
- Alice chooses a random integer a (her private key) and computes A = aG (her public key). This scalar multiplication on the curve replaces the modular exponentiation in the original protocol.
- Bob similarly chooses a random integer b and computes B = bG.
- Alice and Bob exchange their public keys A and B.
- Alice computes the shared secret S = aB, while Bob computes S = bA.
The magic of elliptic curves ensures that aB = abG = bA, so Alice and Bob now share the secret point S without ever directly exchanging it.
The security of ECDH relies on the Elliptic Curve Discrete Logarithm Problem (ECDLP). Even if an eavesdropper sees the public keys A and B, they can’t feasibly determine the private keys a or b, just as in the original Diffie-Hellman.
The key advantage of ECDH over the original Diffie-Hellman is efficiency. ECDH can provide the same level of security as traditional Diffie-Hellman but with significantly smaller key sizes. This makes ECDH particularly suitable for constrained environments like mobile devices or embedded systems.
This upgrade to ECDH demonstrates how changing the underlying mathematical structure – from the multiplicative group of integers modulo a prime to the group of points on an elliptic curve – allows us to maintain and even enhance the security of our key exchange protocol while improving its efficiency.
Conclusion
As our digital world evolves, so will the structures securing our communications. The move to elliptic curves wasn’t just a patch—it was a fundamental upgrade to modern cryptography’s engine, ensuring our digital interactions remain fast and secure.
Maybe one day, we will need to upgrade part of the engine again. Hopefully, researchers in privacy scaling will find an elegant solution to keep cryptography running smoothly.
Acknowledgements
This article was written by Nicolas Biondini, Yago Pajariño, and Arturo Beccar-Varela, as part of their presentation on cryptographic principles during their first week in the Privacy and Scaling Explorations (PSE) Core Program in Buenos Aires, 2024.