The Tension Between Divergence Loss and Profit in Automated Market Makers

Introduction

In the previous two posts (a and b) we discussed how the automated market makers (AMMs) of Balancer, Curve, and Uniswap work. In today’s post we take the perspective of a liquidity provider (LP) and ask: how much you can expect to earn by providing tokens to the reserve pools. To answer this question, we get into the topics of divergence loss (or impermanent loss), fees, and yield farming. We gather some already known facts about these topics presented in [1], [2], [3], and illustrate them based on concrete data of exchange statistics.

Table of Contents

Divergence Loss

The divergence loss (also sometimes called impermanent loss), is a phenomenon which happens to liquidity providers of almost all crypto tokens. It is very important to have this possible investment loss in mind before getting involved into the liquidity provision game. So, let’s try to quickly get the idea of what this is about. Recall that liquidity providers can deposit their tokens to a token pair t₁ and t₂. Once they have done their deposit to both reserves R₁ and R₂, they hold a share b of the total reserve, that is, they hold the share bR₁ of R₁ and the share bR₂ of reserve R₂. (N.B.: In Balancer that might not be the same b for both reserves.)

Liquidity providers can withdraw their share at any time, but in the meanwhile they earn a profit from trading fees or yield farming. That sounds like a great deal, but while providing liquidity they run the risk of having a decrease in value of their investment.

Let’s consider the case of Uniswap where the market maker is determined by the constant product formula of the two reserve pools R₁ and R₂. Denoting by m_u the marginal price of token t₁ expressed in t₂ (e.g. WBTC in ETH), the portfolio value of total reserve for this token pair is just p_v(R₁,R₂) = m_uR₁ + R₂. Interestingly, as soon as the reserves are updated due to a trade and the price m_u of token t₁ moves from the original price, the portfolio value p_v, and so liquidity providers’ shares, makes a loss. This loss is called the divergence loss and is defined by

d = (p_v(R₁^new,R₂^new) – p_v(R₁,R₂)) / p_v(R₁,R₂) .

The new portfolio value can be calculated by the updated reserve sizes and using the formula for the new marginal price, as described in our previous post. In [1] and [2], the divergence loss was already studied, and we cite here the compact formula they provide:

d = 2 * sqrt(r)/(1+ r) – 1,

where r is the ratio m_u^new / m_u of the new and the original token price of t₁. What becomes clear form the divergence loss formula is that as soon as the price moves away from the original price, the portfolio makes a loss (see Figure 1), and so the share of the LP compared to just holding the original funds. Only when the price is back to the original price, i.e. when r = 1, the loss is zero.

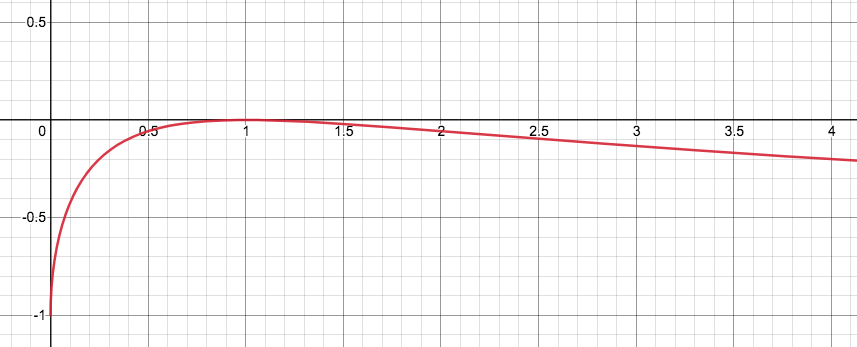
**Figure 1**: Divergence loss with respect to the price ratio of new and old price.

Let’s look at a concrete example to understand how the divergence loss impacts the holding of a liquidity provider.

EXAMPLE: We take the WBTC-ETH coin pair of Uniswap as an example. If we suppose that a liquidity provider would have deposited tokens to the WBTC-ETH pair on January 26th (5pm UTC) with WBTC at 23.884 ETH, and would have withdrawn his deposits from the reserves on March 18th (1 am UTC) with WBTC at 32.884 ETH, then the price ratio r is equal to 1.34152570759. Plugging this value in the formula to calculate the divergence loss, leads to a loss of 1,06% compared to a HODL strategy, i.e. just keeping the WBTC and ETH.

Return through Fees and Yield Farming

There are two possible incomes which can compensate for the potential loss a liquidity provider may have: one is coming from fees and the other is the income from yield farming.

Return from Fees

Each trade costs a fee which increases the reserves (because more goes in than out). This fee f is often about 0.3%. Let’s consider when one trade happens and a trader sells ∆₁ tokens. The new price (see our first article for more about the price impact function g) is m_u^new= g(-∆₁) and the difference of the new AMM portfolio value and the new value of the old reserves is

(m_u^new(R₁ + ∆₁) + R₂ – ∆₂) – (m_u^new R₁ + R₂) = m_u^new∆₁ – ∆₂.

The earned fees are at least f * m_u^new *∆₁, hence a sufficient condition to make no loss is

f *m_u^new * ∆₁ > m_u^new * ∆₁ – ∆₂ > curv * ∆₁²

where curv is the curvature of the AMM (see [3] for more details about the second inequality). We give a concrete example of the curvature below, so it is not so important to give its precise definition. But the last statement is equivalent to

∆₁ < m_u^new* f / curv .

That is to say, that whenever a trade is smaller than the right-hand side, the LP makes a profit on that trade. Certainly, if the price, as mentioned in the first section, comes back to its original price, than the loss disappears and all collected fees become profit. The rule here is that the smaller the curvature of the trading function is, the bigger the trade can become while still guaranteeing a profit.

EXAMPLE: Let’s look again at the Uniswap market, and more specifically, at a stablecoin-stablecoin pair. As of March 18, the USDC-USDT pair had 37,445,575 USDC and 37,456,442 USDT. The curvature for stablecoin pairs is basically curv = 4/p_v (R₁ , R₂) and m_u^new = g(-∆₁) = R₁R₂ / (R₁+∆₁)² . Suppose that a trade of 10,000 USDC occurs. Let’s check whether the sufficient condition for LP profit holds. We can assume that the marginal price is roughly m_u=1. Therefore, we get curv = 5.34e-8 and m_u^new = 0.99975615829. The right-hand side of the above inequality is 21,051 with a percentage fee of 0.03. Since 10,000 is smaller than 21,051 the trade brings a profit to the LPs.

Now, suppose that a trade of 100,000 USDC occurs. The curvature stays the same but m_u^new becomes 0.99496889845. In this case the right-hand side of the inequality is 19736, and the sufficient condition fails to hold, i.e. LPs would make negative profit due to higher divergence loss than earnings from fees. Note that in the case of stablecoins, the price will be corrected by an arbitrageur, so the impermanent loss does not become permanent. But other coins will change their price due to volatility, and the divergence loss becomes a real issue!

Yield Farming

Yet another income for LPs can come from yield farming which made the entire idea of providing liquidity so popular. Yield farming subsidizes the provision of liquidity whereby LPs receive new issued crypto asset, e.g. usable for voting in governance protocols. Accordingly to the share a LP deposits into the reserves, and let these shares locked, (s)he receives these new tokens which can be traded and have their proper value. These tokens can make an interesting extra by “staking” the coins.

In [3], section 3, you can find a thorough analysis about the necessary incentive system using yield farming strategies in order to attract LPs to provide liquidity.