Introduction
Our last blog post discussed the basic mechanisms of the automated market makers (AMMs) in Uniswap, Balancer, and Curve. These projects have achieved to construct purely peer-to-peer exchanges which do not require any intermediary, and attracted already many users (e.g. Uniswap has a total of $4.12 B in its exchange). The essential ideas behind their solutions are based on reserve pools to provide liquidity to the exchange, and to make use of simple mathematical formulas for price discovery. We invite you to read our previous post to get more background about this matter, if needed.
The fact that these AMMs provide – by their nature – token prices onchain, has invited other DeFi projects to make use of them as price oracles. Instead of consulting external exchanges for token prices via price oracles such as Chainlink, it is a more economic and simpler solution to consume the data from, for example, the Uniswap Version 2 AMM. The lending platform Compound for example makes use of Uniswap, although not directly as a price oracle. It is important to bear in mind that things could go wrong when using AMMs naively as a price oracle (read here). One aspect of it is the possibility to manipulate the prices by making large trades due to deterministic slippage effects. These trades can be reverted incurring little cost, and in the meanwhile other DeFi projects may take the altered price paying out a profit to the attacker.
The cost of price manipulation depends on the sizes of the reserves and the formula defining the mechanism of the AMM. We will recall the cost of manipulation for Uniswap derived in [2], and extend it to the case of Balancer. In the last section we evaluate the findings with actual exchange data. If you are not interested in the derivation of the mathematical formulas, you can skip the middle part and jump right away to the discussion part.
A Quick Recap of Uniswap and Balancer
In both protocols, Uniswap and Balancer, liquidity for trades are provided by so-called liquidity providers who deposit tokens t1 and t2 in a prescribed proportion to reserve pools R1 and R2. Liquidity providers have an interest in depositing tokens, since each executed trade brings them a return from the trading fees. When traders want to buy an amount ∆1 ≤ R1 of token t1, the AMM determines the cost in terms of the amount ∆2 of token t2. This price calculation is achieved by restricting the trading function ψ to be constant, i.e. the trading function has the same value before and after the trade. Mathematically speaking, we require the following equation to hold true
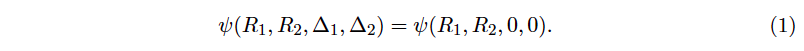
Let’s check what this means in the case of Uniswap and Balancer. The trading function of Uniswap is given by the product of the updated reserves
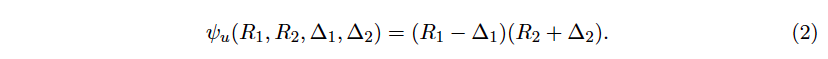
so that the constraint of (2) becomes (R1 – ∆1)(R2 + ∆2) = R1R2. With this at hand, the price of buying ∆1 can be determined as
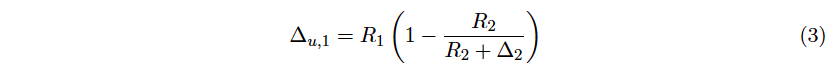
In the case of Balancer, the trading function is given by the weighted product of the reserves
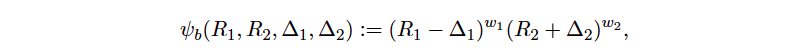
where wi are in the interval [0, 1] such that w1 + w2 = 1. The constraint (2) becomes (R1 – ∆1)w1(R2 + ∆2)w2 = R1w1R2 w2, and the price for 1 is
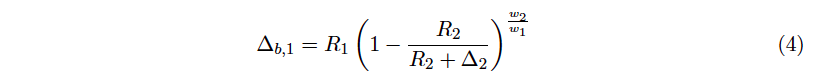
We close this recap by mentioning a result described in our previous post. The marginal prices of the token t1, i.e. the price when performing an infinitesimal small trade where no slippage appears. We found the following formulas for the marginal price mu (Uniswap) and mb (Balancer)
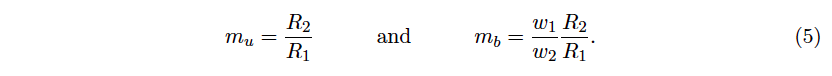
Balancer can be considered to be a generalization of Uniswap, since the choice of w1 =w2 = 1/2 is basically the Uniswap case (taking the square of ψ).
Cost of Price Manipulation in Uniswap
Similarly as above, we start with the mathematical formulation of what the attacker wants to achieve, i.e. an increase of the Balancer AMM price of t1 by adding ∆2 such that mbnew= (1 + ε)mp. Again, by definition of the marginal price, this means
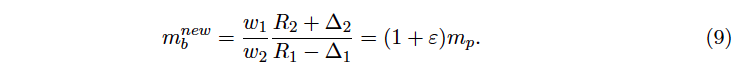
The constraint of satisfying the market maker condition is
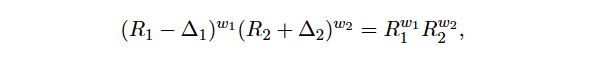
which can be transformed to
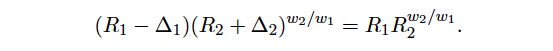
Using the simple relation mb = mp = w1/w2 R2/R1 to get mpR1 = w1/w2 R2, we can derive by multiplying the above equation on both sides of (9)
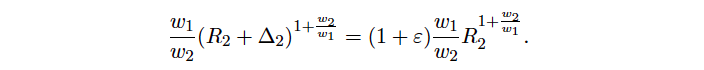
Since 1 + w2/w1 =1/w1 , we get
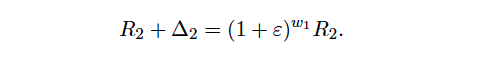
From this we deduce the amount ∆2 to be
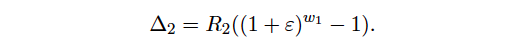
Since the attacker receives in return (plugging ∆2 = R2((1 + ε)w1 – 1) in equation (4))
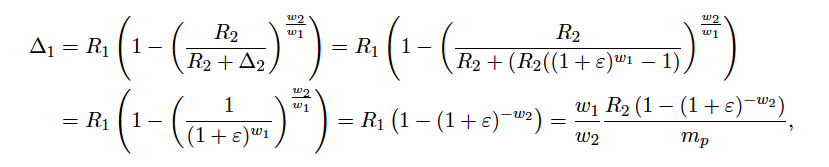
the total cost becomes
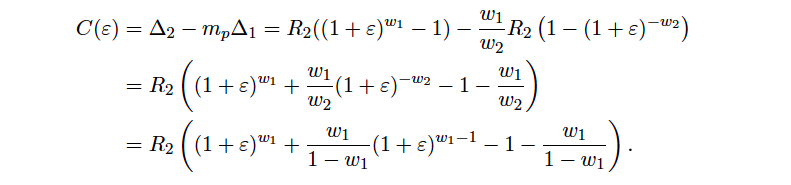
Choosing w1 = 1/2 we get back the cost formula for Uniswap (8).
Evaluation
Now let us interpret the formulas from the previous two sections in two examples by taking data from the Uniswap exchange. The first example takes the reserve size of the WBTC-ETH pair from 9th of March 2021: the pool held 3542 WBTC and 104,823 ETH with a total liquidity of 382,183,185 USD. The following chart shows the manipulation costs ranging from 1 to 100%, and compares the costs to Balancer when choosing w1 = 1/4 and w1 = 3/4.
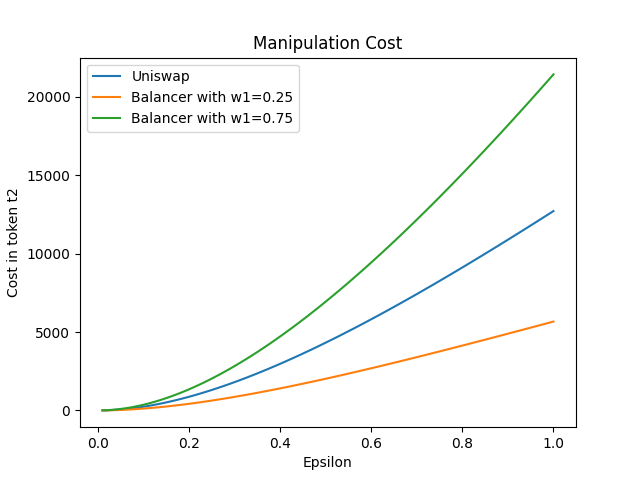
For example, taking the ETH price of 1823 USD as of March 9th, a change of WBTC price in Uniswap would have incurred a minimum costs of:
| Percentage\Cost | Uniswap | Balancer (w1 = 3/4) |
| 1 % | 4729 USD | 7106 USD |
| 5 % | 113,728 USD | 171,986 USD |
| 10 % | 434,054 USD | 661,517 USD |
| 50 % | 7,880,925 USD | 12,652,035 USD |
In the second example we consider the case of the token pair Ocean-ETH in Uniswap. The reserve sizes of the Ocean-ETH pair from 9th of March 2021 are: the pools held 1,774,033 Ocean and 1407 ETH. Taking again the ETH price of 1823 USD as of March 9th, a change of Ocean price in Uniswap would have incurred a minimum costs of:
| Percentage\Cost | Uniswap | Balancer (w1 = 3/4) |
| 1 % | 63 USD | 95 USD |
| 5 % | 2177 USD | 2308 USD |
| 10 % | 5826 USD | 8879 USD |
| 50 % | 105,782 USD | 169,823 USD |
The calculated costs presented above are, as mentioned earlier, lower bounds of the real costs since we do not take the trading fees into account. Anyway the results provide the correct order of magnitude of the manipulation costs. It is also important to mention that this are the costs for a one-time change. Keeping this attack over a longer time period will have an accumulated cost, since arbitageurs will take this price changes as an arbitrage opportunity.
It is noticeable that for pairs with a small total liquidity, price manipulations can be achieved with relatively low costs. For example, changing the Ocean price by 5% in Uniswap costs only 2177 USD, and in a similar situation in Balancer a price change woud have just a slightly higher cost of 2308 USD. Hence, using AMMs of Uniswap and Balancer as price oracles must be considered as very risky, especially when the reserve pools have small total liquidity.